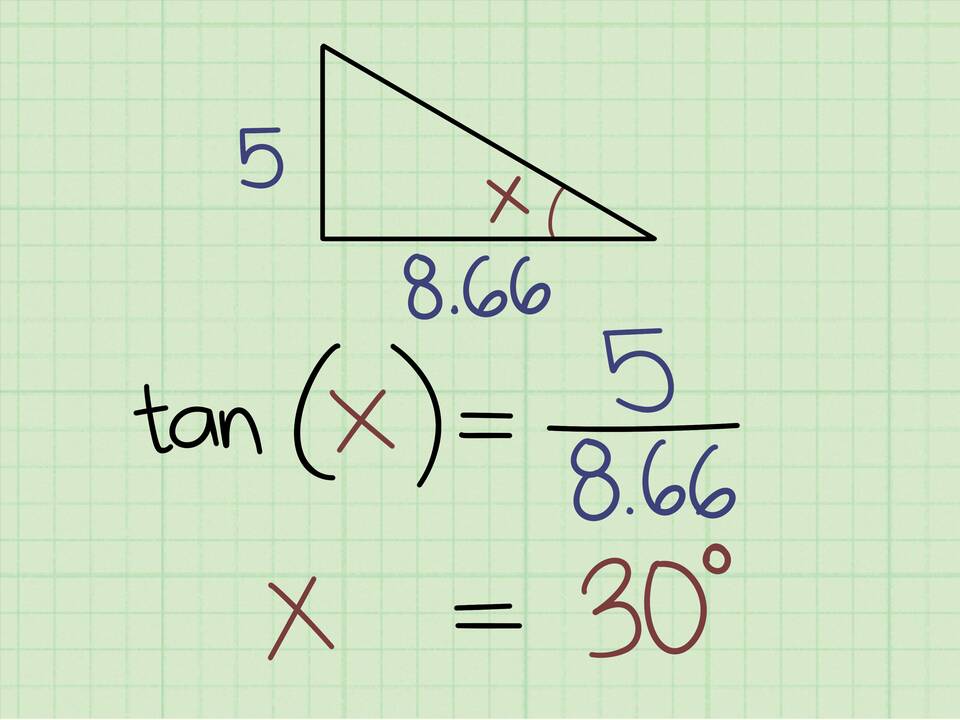В геометрии существуют фундаментальные теоремы о сумме углов различных фигур. Эти знания являются базовыми для решения множества задач в планиметрии и стереометрии.
Содержание
В геометрии существуют фундаментальные теоремы о сумме углов различных фигур. Эти знания являются базовыми для решения множества задач в планиметрии и стереометрии.
Сумма углов треугольника
Одна из основных теорем евклидовой геометрии утверждает:
- Сумма внутренних углов любого треугольника равна 180°
- Это свойство справедливо для всех типов треугольников
- Доказательство основано на свойствах параллельных прямых
| Тип треугольника | Пример углов | Сумма |
| Остроугольный | 60°, 60°, 60° | 180° |
| Прямоугольный | 30°, 60°, 90° | 180° |
| Тупоугольный | 100°, 40°, 40° | 180° |
Сумма внешних углов треугольника
Каждый внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Сумма трех внешних углов составляет 360°.
Сумма углов многоугольников
Для произвольного n-угольника действует формула:
- Сумма внутренних углов = (n - 2) × 180°
- Сумма внешних углов всегда равна 360°
Примеры для различных фигур:
- Четырехугольник: (4-2)×180° = 360°
- Пятиугольник: (5-2)×180° = 540°
- Шестиугольник: (6-2)×180° = 720°
Применение в задачах
Знание суммы углов позволяет:
- Находить неизвестные углы фигур
- Доказывать равенство треугольников
- Решать задачи на построение
- Анализировать свойства многоугольников
Исключения и особые случаи
В неевклидовых геометриях сумма углов треугольника может отличаться от 180°:
- В сферической геометрии сумма больше 180°
- В геометрии Лобачевского сумма меньше 180°
